Perform One-Dimensional Cubic Spline Interpolation using M-relation. More...

Collaboration diagram for CubicSplineEvaluator< T >:

Public Member Functions
	CubicSplineEvaluator (T dist, T dL)

template<typename T1 >
T1	cubicInterpolate (T1 y1, T1 y2, T1 d2y1, T1 d2y2) const

template<typename T1 >
T1	cubicInterpolateSecondDeriv (T1 y1, T1 y2, T1 d2y1, T1 d2y2, T1 &du, T1 &d2u) const

Private Attributes
T	dist

T	dL

T	dLinv

T	cL

T	cR

T	h6

T	q1

T	q2

T	dq1

T	dq2

Detailed Description

template<class T>
class qmcplusplus::CubicSplineEvaluator< T >

Perform One-Dimensional Cubic Spline Interpolation using M-relation.

Given a function evaluated on a grid 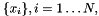$\{x_i\}, i=1\ldots N,$ such that 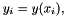$ y_i = y(x_i), $ we would like to interpolate for a point 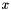$ x $ in the interval $[x_j,x_{j+1}].$ The linear interpolation formula

$y = Ay_j + By_{j+1}$

where

$A = \frac{x_{j+1}-x}{x_{j+1}-x_j} \;\;\;\;\;\;\;\;\;\;\;\;\; B = 1-A = \frac{x-x_{j+1}}{x_{j+1}-x_j}$

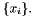Satisfies the conditions at the endpoints $x_j \mbox{ and } x_{j+1},$ but suffers from some major drawbacks. The problem with this approach is that over the range of the function $ [x_1,x_N] $ we have a series of piecewise linear equations with a zero second derivative within each interval and an undefined or infinite second derivative at the interval boundaries, the grid points $\{x_i\}.$ Ideally we would like to construct an interpolation function with a smooth first derivative and a continuous second derivative both within the intervals and at the the grid points.

By adding a cubic polynomial to the linear interpolation equation within each interval, we can construct an interpolation function that varies linearly in the second derivative. Assume for a moment that we have the values of the second derivative evaluated at each grid point, 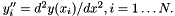$y_i'' = d^2y(x_i)/dx^2, i=1\ldots N.$ Now we can construct a cubic polynomial that has the correct second derivatives 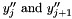$y_j'' \mbox{ and } y_{j+1}''$ at the endpoints and also evaluates to zero at the endpoints. The reason the polynomial must be zero at the endpoints is to not spoil the agreement that is already built into the linear function. A function constructed from these principals is given by the equation

$y = Ay_j + By_{j+1} + Cy_j'' + Dy_{j+1}''$

where

$C = \frac{1}{6}(A^3-A)(x_{j+1}-x_j)^2 \;\;\;\;\;\;\; D = \frac{1}{6}(B^3-B)(x_{j+1}-x_j)^2.$

To explicitly check that this function does indeed satisfy the conditions at the endpoints take the derivatives

$\frac{dy}{dx} = \frac{y_{j+1}-y_j}{x_{j+1}-x_j} - \frac{3A^2-1}{6}(x_{j+1}-x_j)y_j'' + \frac{3B^2-1}{6}(x_{j+1}-x_j)y_{j+1}''$

and

$\frac{d^2y}{dx^2} = Ay_j'' + By_{j+1}''.$

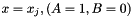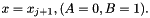
The second derivative is continuous across the boundary between two intervals, e.g. $[x_{j-1},x_j]$ and $[x_j,x_{j+1}],$ and obeys the conditions at the endpoints since at $ x=x_j, (A=1,B=0) $ and at $x=x_{j+1}, (A=0,B=1).$

We had made the assumption that the values of the second derivative are known at the grid points, which they are not. By imposing the condition that the first derivative is smooth and continuous across the boundary between two intervals it is possible to derive a set of equations to generate the 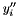$ y_i''$ 's. Evaluate the equation for the first derivative at $x=x_j$ in the inverval $[x_{j-1},x_j]$ and set it equal to the same equation evaluated at $x=x_j$ in the inverval $[x_j,x_{j+1}];$ rearranging the terms

$\frac{x_j-x_{j+1}}{6}y_{j+1}'' + \frac{x_{j+1}-x_{j-1}}{3}y_j'' + \frac{x_{j+1}-x_j}{6}y_{j+1}'' = \frac{y_{j+1}-y_j}{x_{j+1}-x_j} - \frac{y_j-y_{j+1}}{x_j-x_{j+1}},$

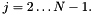where $j=2\ldots N-1.$ To generate a unique solution for the system of 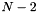$N-2$ equations we have to impose boundary conditions at 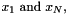$x_1 \mbox{ and } x_N,$ the possibilities being either to set 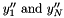$y_1'' \mbox{ and } y_N''$ to zero, the natural cubic spline, or, if you want to make the first derivative at the boundaries to have a specified value, use 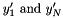$y_1' \mbox{ and } y_N'$ to calculate the second derivatives at the endpoints using equation.

Definition at line 110 of file OneDimCubicSpline.h.

Constructor & Destructor Documentation

◆ CubicSplineEvaluator()

CubicSplineEvaluator	(	T	dist,
		T	dL
	)

inline

Definition at line 125 of file OneDimCubicSpline.h.

References CubicSplineEvaluator< T >::cL, CubicSplineEvaluator< T >::cR, CubicSplineEvaluator< T >::dist, CubicSplineEvaluator< T >::dL, CubicSplineEvaluator< T >::dLinv, CubicSplineEvaluator< T >::dq1, CubicSplineEvaluator< T >::dq2, CubicSplineEvaluator< T >::h6, CubicSplineEvaluator< T >::q1, and CubicSplineEvaluator< T >::q2.

   {
     dLinv = 1.0 / dL;
     cL    = dist * dLinv;
     cR    = (dL - dist) * dLinv;
     h6    = dL / 6.0;
     q1    = cR * (cR * cR - 1.0) * h6 * dL;
     q2    = cL * (cL * cL - 1.0) * h6 * dL;
     dq1   = h6 * (1.0 - 3.0 * cR * cR);
     dq2   = h6 * (3.0 * cL * cL - 1.0);
   }

Member Function Documentation

◆ cubicInterpolate()

T1 cubicInterpolate	(	T1	y1,
		T1	y2,
		T1	d2y1,
		T1	d2y2
	)		const

inline

Definition at line 138 of file OneDimCubicSpline.h.

References CubicSplineEvaluator< T >::cL, CubicSplineEvaluator< T >::cR, CubicSplineEvaluator< T >::q1, and CubicSplineEvaluator< T >::q2.

Referenced by OneDimCubicSplineLinearGrid< T >::splint(), and OneDimCubicSpline< T >::splint().

   {
     return cR * y1 + cL * y2 + q1 * d2y1 + q2 * d2y2;
   }

◆ cubicInterpolateSecondDeriv()

T1 cubicInterpolateSecondDeriv	(	T1	y1,
		T1	y2,
		T1	d2y1,
		T1	d2y2,
		T1 &	du,
		T1 &	d2u
	)		const

inline

Definition at line 144 of file OneDimCubicSpline.h.

References CubicSplineEvaluator< T >::cL, CubicSplineEvaluator< T >::cR, CubicSplineEvaluator< T >::dLinv, CubicSplineEvaluator< T >::dq1, CubicSplineEvaluator< T >::dq2, CubicSplineEvaluator< T >::q1, and CubicSplineEvaluator< T >::q2.

Referenced by OneDimCubicSpline< T >::splint().

   {
     du  = dLinv * (y2 - y1) + dq1 * d2y1 + dq2 * d2y2;
     d2u = cR * d2y1 + cL * d2y2;
     return cR * y1 + cL * y2 + q1 * d2y1 + q2 * d2y2;
   }