a class that defines a supercell in D-dimensional Euclean space. More...

Inheritance diagram for CrystalLattice< T, D >:

Collaboration diagram for CrystalLattice< T, D >:

Public Types
enum	{ DIM = D }
	enumeration for the dimension of the lattice More...

using	Base = LRBreakupParameters< T, D >
	alias to the base class More...


using	Scalar_t = T
	the type of scalar More...

using	SingleParticlePos = TinyVector< T, D >
	the type of a D-dimensional position vector More...

using	SingleParticleIndex = TinyVector< int, D >
	the type of a D-dimensional index vector More...

using	Tensor_t = Tensor< T, D >
	the type of a D-dimensional Tensor More...

Public Member Functions
	CrystalLattice ()
	default constructor, assign a huge supercell More...

SingleParticlePos	a (int i) const
	Provide interfaces familiar to fotran users. More...

SingleParticlePos	b (int i) const
	Provide interfaces familiar to fotran users. More...

template<class T1 >
SingleParticlePos	toUnit (const TinyVector< T1, D > &r) const
	Convert a cartesian vector to a unit vector. More...

template<class T1 >
SingleParticlePos	toUnit_floor (const TinyVector< T1, D > &r) const

template<class T1 >
SingleParticlePos	toCart (const TinyVector< T1, D > &c) const
	Convert a unit vector to a cartesian vector. More...

bool	isValid (const TinyVector< T, D > &u) const
	return true if all the open direction of reduced coordinates u are in the range [0,1) More...

bool	outOfBound (const TinyVector< T, D > &u) const
	return true if any direction of reduced coordinates u goes larger than 0.5 More...

void	applyMinimumImage (TinyVector< T, D > &c) const

T	Dot (const SingleParticlePos &ra, const SingleParticlePos &rb) const
	evaluate the cartesian distance More...

SingleParticlePos	k_cart (const SingleParticlePos &kin) const
	conversion of a reciprocal-vector More...

SingleParticlePos	k_unit (const SingleParticlePos &kin) const
	conversion of a caresian reciprocal-vector to unit k-vector More...

T	ksq (const SingleParticlePos &kin) const
	evaluat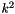e More...

template<typename T1 >
CrystalLattice< T, D > &	operator= (const CrystalLattice< T1, D > &rhs)
	assignment operator More...

CrystalLattice< T, D > &	operator*= (T sc)
	scale the lattice vectors by sc. More...

template<class TT >
void	set (const Tensor< TT, D > &lat)
	set the lattice vector from the command-line options More...

void	reset ()
	Evaluate the reciprocal vectors, volume and metric tensor. More...

void	print (std::ostream &, int level=2) const
	Print out CrystalLattice Data. More...

Public Attributes
bool	DiagonalOnly
	true, if off-diagonal elements are zero so that other classes can take advantage of this More...

int	SuperCellEnum
	supercell enumeration More...

TinyVector< int, D >	BoxBConds
	The boundary condition in each direction. More...

T	VacuumScale
	The scale factor for adding vacuum. More...

SingleParticlePos	ABC

bool	explicitly_defined
	true, the lattice is defined by the input instead of an artificial default More...


Scalar_t	Volume
	Physical properties of a supercell. More...

Scalar_t	WignerSeitzRadius
	Wigner-Seitz cell radius. More...

Scalar_t	SimulationCellRadius
	simulation cell radii More...

Scalar_t	CellRadiusSq
	SimulationCellRadius*SimulationCellRadius. More...

Scalar_t	WignerSeitzRadius_G
	Wigner-Seitz cell radius in reciprocal space. More...

Tensor_t	R
	Real-space unit vectors. R(i,j) i=vector and j=x,y,z. More...

Tensor_t	G
	Reciprocal unit vectors. G(j,i) i=vector and j=x,y,z. More...

Tensor_t	Gt
	Transpose of reciprocal unit vectors: More...

Tensor_t	M
	Metric tensor. More...

Tensor_t	Mg
	Metric tensor for G vectors. More...

SingleParticlePos	Length
	Length[idim] length of the idim-th lattice vector. More...

SingleParticlePos	OneOverLength
	OneOverLength[idim] 1/length of the idim-th lattice vector. More...

SingleParticlePos	Center
	Center of the cell sum(Rv[i])/2. More...

TinyVector< SingleParticlePos, D >	Rv
	Real-space unit vectors. More...

TinyVector< SingleParticlePos, D >	Gv
	Reciprocal unit vectors. More...

Detailed Description

template<class T, unsigned D>
struct qmcplusplus::CrystalLattice< T, D >

a class that defines a supercell in D-dimensional Euclean space.

CrystalLattice handles the physical properties of a supercell, such as lattice vectors, reciprocal vectors and metric tensors and provides interfaces to access the lattice properties and convert units of position vectors or a single-particle position from Cartesian to Lattice Unit vice versa.

Definition at line 55 of file CrystalLattice.h.

Member Typedef Documentation

◆ Base

using Base = LRBreakupParameters<T, D>

alias to the base class

Definition at line 58 of file CrystalLattice.h.

◆ Scalar_t

using Scalar_t = T

the type of scalar

Definition at line 67 of file CrystalLattice.h.

◆ SingleParticleIndex

using SingleParticleIndex = TinyVector<int, D>

the type of a D-dimensional index vector

Definition at line 71 of file CrystalLattice.h.

◆ SingleParticlePos

using SingleParticlePos = TinyVector<T, D>

the type of a D-dimensional position vector

Definition at line 69 of file CrystalLattice.h.

◆ Tensor_t

using Tensor_t = Tensor<T, D>

the type of a D-dimensional Tensor

Definition at line 73 of file CrystalLattice.h.

Member Enumeration Documentation

◆ anonymous enum

anonymous enum

enumeration for the dimension of the lattice

Enumerator
DIM

Definition at line 61 of file CrystalLattice.h.

   {
     DIM = D
   };

Constructor & Destructor Documentation

◆ CrystalLattice()

CrystalLattice ( )

default constructor, assign a huge supercell

Default constructor. Initialized to a 1x1x1 cubic supercell.

Definition at line 29 of file CrystalLattice.cpp.

 {
   explicitly_defined = false;
   BoxBConds          = 0;
   VacuumScale        = 1.0;
   R.diagonal(1e10);
   G      = R;
   M      = R;
   Volume = 1;
   reset();
 }

Member Function Documentation

◆ a()

SingleParticlePos a ( int i ) const

inline

Provide interfaces familiar to fotran users.

Parameters

i	the index of the directional vector, 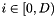$i\in [0,D)$

Returns: The lattice vector of the ith direction

Definition at line 137 of file CrystalLattice.h.

Referenced by DTD_BConds< T, 3, PPPG >::DTD_BConds(), DTD_BConds< T, 3, PPNG >::DTD_BConds(), DTD_BConds< T, 3, PPPG+SOA_OFFSET >::DTD_BConds(), and DTD_BConds< T, 3, PPNG+SOA_OFFSET >::DTD_BConds().

137 { return Rv[i]; }

qmcplusplus::CrystalLattice::Rv

TinyVector< SingleParticlePos, D > Rv

Real-space unit vectors.

Definition: CrystalLattice.h:117

◆ applyMinimumImage()

void applyMinimumImage ( TinyVector< T, D > & c ) const

inline

Definition at line 194 of file CrystalLattice.h.

   {
     if (SuperCellEnum)
     {
       TinyVector<T, D> u = dot(c, G);
       for (int i = 0; i < D; ++i)
         u[i] = u[i] - round(u[i]);
       c = dot(u, R);
     }
   }

◆ b()

SingleParticlePos b ( int i ) const

inline

Provide interfaces familiar to fotran users.

Parameters

i	the index of the directional vector, 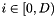$i\in [0,D)$

Returns: The reciprocal vector of the ith direction

Definition at line 143 of file CrystalLattice.h.

143 { return Gv[i]; }

qmcplusplus::CrystalLattice::Gv

TinyVector< SingleParticlePos, D > Gv

Reciprocal unit vectors.

Definition: CrystalLattice.h:123

◆ Dot()

T Dot	(	const SingleParticlePos &	ra,
		const SingleParticlePos &	rb
	)		const

inline

evaluate the cartesian distance

Parameters

ra	a vector in the supercell unit
rb	a vector in the supercell unit

Returns: Cartesian distance with two vectors in SC unit

Note: The distance between two cartesian vectors are handled by dot function defined in OhmmsPETE/TinyVector.h

Definition at line 213 of file CrystalLattice.h.

213 { return dot(ra, dot(M, rb)); }

qmcplusplus::CrystalLattice::M

Tensor_t M

Metric tensor.

Definition: CrystalLattice.h:103

qmcplusplus::dot

Tensor< typename BinaryReturn< T1, T2, OpMultiply >::Type_t, D > dot(const AntiSymTensor< T1, D > &lhs, const AntiSymTensor< T2, D > &rhs)

Definition: AntiSymTensor.h:520

◆ isValid()

bool isValid ( const TinyVector< T, D > & u ) const

inline

return true if all the open direction of reduced coordinates u are in the range [0,1)

Definition at line 177 of file CrystalLattice.h.

Referenced by ParticleSet::makeMoveAllParticles(), ParticleSet::makeMoveAllParticlesWithDrift(), ParticleSet::makeMoveAndCheck(), and qmcplusplus::TEST_CASE().

   {
     bool inside = true;
     for (int dim = 0; dim < D; dim++)
       inside &= (BoxBConds[dim] || (u[dim] >= T(0) && u[dim] < T(1)));
     return inside;
   }

◆ k_cart()

SingleParticlePos k_cart ( const SingleParticlePos & kin ) const

inline

conversion of a reciprocal-vector

Parameters

kin	an input reciprocal vector in the Reciprocal-vector unit

Returns: k(reciprocal vector) in cartesian unit

Definition at line 219 of file CrystalLattice.h.

Referenced by EinsplineSetBuilder::AnalyzeTwists2(), BsplineReader::check_twists(), Gvectors< ST, LT >::Gvectors(), BsplineReader::initialize_spo2band(), MomentumDistribution::MomentumDistribution(), MomentumEstimator::putSpecial(), PWBasis::readbasis(), and PWBasis::trimforecut().

219 { return TWOPI * dot(G, kin); }

qmcplusplus::CrystalLattice::G

Tensor_t G

Reciprocal unit vectors. G(j,i) i=vector and j=x,y,z.

Definition: CrystalLattice.h:99

qmcplusplus::dot

Tensor< typename BinaryReturn< T1, T2, OpMultiply >::Type_t, D > dot(const AntiSymTensor< T1, D > &lhs, const AntiSymTensor< T2, D > &rhs)

Definition: AntiSymTensor.h:520

◆ k_unit()

SingleParticlePos k_unit ( const SingleParticlePos & kin ) const

inline

conversion of a caresian reciprocal-vector to unit k-vector

Parameters

kin	an input reciprocal vector in cartesian form

Returns: k(reciprocal vector) as unit vector

Definition at line 225 of file CrystalLattice.h.

225 { return dot(R, kin) / TWOPI; }

qmcplusplus::dot

Tensor< typename BinaryReturn< T1, T2, OpMultiply >::Type_t, D > dot(const AntiSymTensor< T1, D > &lhs, const AntiSymTensor< T2, D > &rhs)

Definition: AntiSymTensor.h:520

qmcplusplus::CrystalLattice::R

Tensor_t R

Real-space unit vectors. R(i,j) i=vector and j=x,y,z.

Definition: CrystalLattice.h:97

◆ ksq()

T ksq ( const SingleParticlePos & kin ) const

inline

evaluate 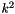$k^2$

Parameters

kin	an input reciprocal vector in reciprocal-vector unit

Returns: $k_{in}^2$

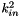
Definition at line 232 of file CrystalLattice.h.

232 { return dot(kin, dot(Mg, kin)); }

qmcplusplus::dot

Tensor< typename BinaryReturn< T1, T2, OpMultiply >::Type_t, D > dot(const AntiSymTensor< T1, D > &lhs, const AntiSymTensor< T2, D > &rhs)

Definition: AntiSymTensor.h:520

qmcplusplus::CrystalLattice::Mg

Tensor_t Mg

Metric tensor for G vectors.

Definition: CrystalLattice.h:105

◆ operator*=()

CrystalLattice< T, D > & operator*= ( T sc )

scale the lattice vectors by sc.

Rescale this supercell by a scalar.

All the internal data are reset.

Parameters

sc	the scaling value

Returns: a new CrystalLattice

Parameters

sc	A scaling factor.

Definition at line 95 of file CrystalLattice.cpp.

 {
   R *= sc;
   reset();
   return *this;
 }

◆ operator=()

CrystalLattice<T, D>& operator= ( const CrystalLattice< T1, D > & rhs )

inline

assignment operator

Definition at line 236 of file CrystalLattice.h.

   {
     Base::LR_dim_cutoff         = rhs.LR_dim_cutoff;
     Base::LR_kc                 = rhs.LR_kc;
     Base::LR_rc                 = rhs.LR_rc;
     Base::num_ewald_grid_points = rhs.num_ewald_grid_points;
     Base::ndim                  = rhs.ndim;
 
     explicitly_defined = rhs.explicitly_defined;
     BoxBConds          = rhs.BoxBConds;
     VacuumScale        = rhs.VacuumScale;
     R                  = rhs.R;
     reset();
     return *this;
   }

◆ outOfBound()

bool outOfBound ( const TinyVector< T, D > & u ) const

inline

return true if any direction of reduced coordinates u goes larger than 0.5

Definition at line 186 of file CrystalLattice.h.

Referenced by ParticleSet::makeMoveAllParticles(), ParticleSet::makeMoveAllParticlesWithDrift(), ParticleSet::makeMoveAndCheck(), and qmcplusplus::TEST_CASE().

   {
     for (int i = 0; i < D; ++i)
       if (std::abs(u[i]) > 0.5)
         return true;
     return false;
   }

◆ print()

void print	(	std::ostream &	os,
		int	level = `2`
	)		const

Print out CrystalLattice Data.

Definition at line 103 of file CrystalLattice.cpp.

Referenced by SimulationCell::resetLRBox().

 {
   /*\note level == 0: print only the lattice vectors
    *      level == 1: lattice vectors, boundary conditions, grid
    *      level == 2: + all the internal values
    */
   std::string unit_name = "bohr";
 
   std::string lattice_name = "  Lattice (" + unit_name + "):";
   std::string pad(lattice_name.length(), ' ');
   os << lattice_name;
   for (int i = 0; i < D; ++i)
   {
     if (i > 0)
     {
       os << pad;
     }
     os << Rv[i] << std::endl;
   }
   if (level > 0)
   {
     os << std::endl;
     os << "  Boundary Conditions: ";
     for (int i = 0; i < D; ++i)
     {
       if (BoxBConds[i])
         os << " p ";
       else
         os << " n ";
     }
     os << std::endl;
     if (VacuumScale != 1.0)
       os << "  Vacuum scale: " << VacuumScale << std::endl;
   }
   if (level > 1)
   {
     os << std::endl;
     os << "  Volume (bohr^3) = " << Volume << std::endl;
     os << std::endl;
     os << "  Reciprocal vectors without 2*pi.\n";
     for (int i = 0; i < D; ++i)
       os << "    g_" << i + 1 << " = " << Gv[i] << std::endl;
     os << std::endl;
     os << "  Metric tensor in real-space.\n";
     for (int i = 0; i < D; ++i)
     {
       os << "    h_" << i + 1 << " = ";
       for (int j = 0; j < D; ++j)
       {
         os << M(i, j) << " ";
       }
       os << std::endl;
     }
     os << std::endl;
     os << "  Metric tensor in g-space.\n";
     for (int i = 0; i < D; ++i)
     {
       os << "    h_" << i + 1 << " = ";
       for (int j = 0; j < D; ++j)
       {
         os << Mg(i, j) << " ";
       }
       os << std::endl;
     }
   }
 }

◆ reset()

void reset ( )

Evaluate the reciprocal vectors, volume and metric tensor.

Definition at line 51 of file CrystalLattice.cpp.

Referenced by OneBodyDensityMatrices::OneBodyDensityMatrices(), CrystalLattice< ST, 3 >::operator=(), SimulationCell::resetLRBox(), and qmcplusplus::TEST_CASE().

 {
   G      = inverse(R); //G = transpose(Inverse(R));
   Gt     = transpose(G);
   Volume = std::abs(det(R));
   //M = dot(transpose(R),R);
   M   = dot(R, transpose(R));
   T t = TWOPI * TWOPI;
   Mg  = t * dot(transpose(G), G);
   for (int i = 0; i < D; ++i)
     for (int j = 0; j < D; ++j)
       Rv[i][j] = R(i, j);
   for (int i = 0; i < D; ++i)
     for (int j = 0; j < D; ++j)
       Gv[i][j] = G(j, i);
   for (int i = 0; i < D; ++i)
   {
     Length[i]        = std::sqrt(dot(Rv[i], Rv[i]));
     OneOverLength[i] = 1.0 / Length[i];
   }
   Center = 0.0;
   for (int i = 0; i < D; ++i)
     Center += Rv[i];
   Center *= .5;
   //analysis of a lattice using LatticeAnalyzer
   LatticeAnalyzer<T, D> ldesc;
   SuperCellEnum        = ldesc(BoxBConds);
   DiagonalOnly         = ldesc.isDiagonalOnly(R);
   ABC                  = ldesc.calcSolidAngles(Rv, OneOverLength);
   WignerSeitzRadius    = ldesc.calcWignerSeitzRadius(Rv);
   WignerSeitzRadius_G  = ldesc.calcWignerSeitzRadius(Gv);
   SimulationCellRadius = ldesc.calcSimulationCellRadius(Rv);
   // set equal WignerSeitzRadius and SimulationCellRadius when they are very close.
   if (WignerSeitzRadius > SimulationCellRadius &&
       WignerSeitzRadius - SimulationCellRadius <= WignerSeitzRadius * std::numeric_limits<float>::epsilon() * 2)
     WignerSeitzRadius = SimulationCellRadius;
   CellRadiusSq = SimulationCellRadius * SimulationCellRadius;
 }

◆ set()

void set ( const Tensor< TT, D > & lat )

set the lattice vector from the command-line options

Parameters

lat	a tensor representing a supercell

Definition at line 43 of file CrystalLattice.cpp.

Referenced by InitMolecularSystem::initWithVolume(), LatticeParser::put(), SpinDensity::put(), OrbitalImages::put(), EinsplineSetBuilder::ReadOrbitalInfo_ESHDF(), SpinDensityInput::readXML(), and EinsplineSetBuilder::set_metadata().

 {
   explicitly_defined = true;
   R                  = lat;
   reset();
 }

◆ toCart()

SingleParticlePos toCart ( const TinyVector< T1, D > & c ) const

inline

Convert a unit vector to a cartesian vector.

Boundary conditions are not applied.

Definition at line 171 of file CrystalLattice.h.

Referenced by MomentumDistribution::accumulate(), MomentumEstimator::evaluate(), OrbitalImages::evaluate(), OneBodyDensityMatrices::generateUniformGrid(), OneBodyDensityMatrices::generateUniformSamples(), and OneBodyDensityMatrices::normalizeBasis().

   {
     return dot(c, R);
   }

◆ toUnit()

SingleParticlePos toUnit ( const TinyVector< T1, D > & r ) const

inline

Convert a cartesian vector to a unit vector.

Boundary conditions are not applied.

Definition at line 149 of file CrystalLattice.h.

Referenced by SpinDensityNew::accumulate(), MagnetizationDensity::computeBin(), SplineR2R< ST >::convertPos(), SpinDensity::evaluate(), ParticleSet::makeMoveAllParticles(), ParticleSet::makeMoveAllParticlesWithDrift(), ParticleSet::makeMoveAndCheck(), SpinDensity::test_evaluate(), and CrystalLattice< ST, 3 >::toUnit_floor().

   {
     return dot(r, G);
   }

◆ toUnit_floor()

SingleParticlePos toUnit_floor ( const TinyVector< T1, D > & r ) const

inline

Definition at line 155 of file CrystalLattice.h.

Referenced by EinsplineSetBuilder::ReadOrbitalInfo_ESHDF().

   {
     SingleParticlePos val_dot;
     val_dot = toUnit(r);
     for (int i = 0; i < D; i++)
       if (-std::numeric_limits<T1>::epsilon() < val_dot[i] && val_dot[i] < 0)
         val_dot[i] = T1(0.0);
       else
         val_dot[i] -= std::floor(val_dot[i]);
     return val_dot;
   }

Member Data Documentation

◆ ABC

SingleParticlePos ABC

Definition at line 126 of file CrystalLattice.h.

◆ BoxBConds

TinyVector<int, D> BoxBConds

The boundary condition in each direction.

Definition at line 81 of file CrystalLattice.h.

Referenced by LatticeXMLWriter::get(), CrystalLattice< ST, 3 >::isValid(), CrystalLattice< ST, 3 >::operator=(), LatticeParser::put(), and qmcplusplus::TEST_CASE().

◆ CellRadiusSq

Scalar_t CellRadiusSq

SimulationCellRadius*SimulationCellRadius.

Definition at line 93 of file CrystalLattice.h.

◆ Center

SingleParticlePos Center

Center of the cell sum(Rv[i])/2.

Definition at line 111 of file CrystalLattice.h.

Referenced by MagnetizationDensity::MagnetizationDensity(), OneBodyDensityMatrices::OneBodyDensityMatrices(), SpinDensity::put(), OrbitalImages::put(), SpinDensity::report(), SpinDensityNew::report(), and OrbitalImages::report().

◆ DiagonalOnly

bool DiagonalOnly

true, if off-diagonal elements are zero so that other classes can take advantage of this

Definition at line 77 of file CrystalLattice.h.

◆ explicitly_defined

bool explicitly_defined

true, the lattice is defined by the input instead of an artificial default

Definition at line 128 of file CrystalLattice.h.

Referenced by ParticleSet::createSK(), ParticleSet::makeMoveAllParticles(), ParticleSet::makeMoveAllParticlesWithDrift(), ParticleSet::makeMoveAndCheck(), CrystalLattice< ST, 3 >::operator=(), EstimatorManagerNew::put(), SpinDensityNew::SpinDensityNew(), and qmcplusplus::TEST_CASE().

◆ G

Tensor_t G

Reciprocal unit vectors. G(j,i) i=vector and j=x,y,z.

Definition at line 99 of file CrystalLattice.h.

Referenced by CrystalLattice< ST, 3 >::applyMinimumImage(), SplineR2R< ST >::create_spline(), DTD_BConds< T, 3, PPNG >::DTD_BConds(), DTD_BConds< T, 3, PPNG+SOA_OFFSET >::DTD_BConds(), SplineC2COMPTarget< ST >::finalizeConstruction(), SplineC2ROMPTarget< ST >::finalizeConstruction(), CrystalLattice< ST, 3 >::k_cart(), EinsplineSetBuilder::set_metadata(), and CrystalLattice< ST, 3 >::toUnit().

◆ Gt

Tensor_t Gt

Transpose of reciprocal unit vectors:

Definition at line 101 of file CrystalLattice.h.

◆ Gv

TinyVector<SingleParticlePos, D> Gv

Reciprocal unit vectors.

Introduced to efficiently return one vector at a time. Gv[i] is D-dim vector of the ith direction.

Definition at line 123 of file CrystalLattice.h.

Referenced by CrystalLattice< ST, 3 >::b(), and MomentumDistribution::MomentumDistribution().

◆ Length

SingleParticlePos Length

Length[idim] length of the idim-th lattice vector.

Definition at line 107 of file CrystalLattice.h.

◆ M

Tensor_t M

Metric tensor.

Definition at line 103 of file CrystalLattice.h.

Referenced by CrystalLattice< ST, 3 >::Dot().

◆ Mg

Tensor_t Mg

Metric tensor for G vectors.

Definition at line 105 of file CrystalLattice.h.

Referenced by CrystalLattice< ST, 3 >::ksq().

◆ OneOverLength

SingleParticlePos OneOverLength

OneOverLength[idim] 1/length of the idim-th lattice vector.

Definition at line 109 of file CrystalLattice.h.

◆ R

Tensor_t R

Real-space unit vectors. R(i,j) i=vector and j=x,y,z.

Definition at line 97 of file CrystalLattice.h.

Referenced by CrystalLattice< ST, 3 >::applyMinimumImage(), LatticeXMLWriter::createNode(), LatticeXMLWriter::get(), CrystalLattice< ST, 3 >::k_unit(), CrystalLattice< ST, 3 >::operator=(), qmcplusplus::operator==(), SimulationCell::resetLRBox(), qmcplusplus::TEST_CASE(), and CrystalLattice< ST, 3 >::toCart().

◆ Rv

TinyVector<SingleParticlePos, D> Rv

Real-space unit vectors.

Introduced to efficiently return one vector at a time. Rv[i] is D-dim vector of the ith direction.

Definition at line 117 of file CrystalLattice.h.

Referenced by CrystalLattice< ST, 3 >::a(), SpinDensity::put(), SpinDensity::report(), SpinDensityNew::report(), OrbitalImages::report(), SimulationCell::resetLRBox(), qmcplusplus::TEST_CASE(), and OrbitalImages::write_orbital_xsf().

◆ SimulationCellRadius

Scalar_t SimulationCellRadius

simulation cell radii

Definition at line 91 of file CrystalLattice.h.

Referenced by LatticeParser::put().

◆ SuperCellEnum

int SuperCellEnum

supercell enumeration

Definition at line 79 of file CrystalLattice.h.

Referenced by CrystalLattice< ST, 3 >::applyMinimumImage(), ParticleSet::createSK(), OneBodyDensityMatrices::OneBodyDensityMatrices(), LatticeParser::put(), SimulationCell::resetLRBox(), and qmcplusplus::TEST_CASE().

◆ VacuumScale

T VacuumScale

The scale factor for adding vacuum.

Definition at line 83 of file CrystalLattice.h.

Referenced by CrystalLattice< ST, 3 >::operator=(), LatticeParser::put(), SimulationCell::resetLRBox(), and qmcplusplus::TEST_CASE().

◆ Volume

Scalar_t Volume

Physical properties of a supercell.

Volume of a supercell

Definition at line 87 of file CrystalLattice.h.

Referenced by LPQHIBasis::Dminus(), LPQHISRCoulombBasis::Dminus(), LPQHISRCoulombBasis::Dminus_dG(), LPQHIBasis::Dplus(), LPQHISRCoulombBasis::Dplus(), LPQHISRCoulombBasis::Dplus_dG(), LRBasis::get_CellVolume(), MomentumDistribution::MomentumDistribution(), OneBodyDensityMatrices::OneBodyDensityMatrices(), and qmcplusplus::TEST_CASE().

◆ WignerSeitzRadius

Scalar_t WignerSeitzRadius

Wigner-Seitz cell radius.

Definition at line 89 of file CrystalLattice.h.

Referenced by LatticeParser::put().

◆ WignerSeitzRadius_G

Scalar_t WignerSeitzRadius_G

Wigner-Seitz cell radius in reciprocal space.

Definition at line 95 of file CrystalLattice.h.

Referenced by MomentumDistribution::MomentumDistribution().

The documentation for this struct was generated from the following files:

/home/pk7/projects/qmc/for_cron_doxygen/qmcpack/src/Particle/Lattice/CrystalLattice.h
/home/pk7/projects/qmc/for_cron_doxygen/qmcpack/src/Particle/Lattice/CrystalLattice.cpp

Public Types

Public Member Functions

Public Attributes

Detailed Description

template<class T, unsigned D> struct qmcplusplus::CrystalLattice< T, D >

Member Typedef Documentation

◆ Base

◆ Scalar_t

◆ SingleParticleIndex

◆ SingleParticlePos

◆ Tensor_t

Member Enumeration Documentation

◆ anonymous enum

Constructor & Destructor Documentation

◆ CrystalLattice()

Member Function Documentation

◆ a()

◆ applyMinimumImage()

◆ b()

◆ Dot()

◆ isValid()

◆ k_cart()

◆ k_unit()

◆ ksq()

◆ operator*=()

◆ operator=()

◆ outOfBound()

◆ print()

◆ reset()

◆ set()

◆ toCart()

◆ toUnit()

◆ toUnit_floor()

Member Data Documentation

◆ ABC

◆ BoxBConds

◆ CellRadiusSq

◆ Center

◆ DiagonalOnly

◆ explicitly_defined

◆ G

◆ Gt

◆ Gv

◆ Length

◆ M

◆ Mg

◆ OneOverLength

◆ R

◆ Rv

◆ SimulationCellRadius

◆ SuperCellEnum

◆ VacuumScale

◆ Volume

◆ WignerSeitzRadius

◆ WignerSeitzRadius_G

template<class T, unsigned D>
struct qmcplusplus::CrystalLattice< T, D >