 |
QMCPACK
|
 |
QMCPACK
|
SphericalTensor that evaluates the Real Spherical Harmonics. More...
 Collaboration diagram for SphericalTensor< T, Point_t, Tensor_t, GGG_t >:
Collaboration diagram for SphericalTensor< T, Point_t, Tensor_t, GGG_t >:Public Types | |
| using | value_type = T |
| using | pos_type = Point_t |
| using | hess_type = Tensor_t |
| using | ggg_type = GGG_t |
| using | This_t = SphericalTensor< T, Point_t > |
Public Member Functions | |
| SphericalTensor (const int l_max, bool addsign=false) | |
| constructor More... | |
| void | evaluate (const Point_t &p) |
makes a table of  and their gradients up to Lmax. More... and their gradients up to Lmax. More... | |
| void | evaluateAll (const Point_t &p) |
makes a table of  and their gradients up to Lmax. More... and their gradients up to Lmax. More... | |
| void | evaluateTest (const Point_t &p) |
makes a table of  and their gradients up to Lmax. More... and their gradients up to Lmax. More... | |
| void | evaluateWithHessian (const Point_t &p) |
makes a table of  and their gradients and hessians up to Lmax. More... and their gradients and hessians up to Lmax. More... | |
| void | evaluateThirdDerivOnly (const Point_t &p) |
makes a table of  and their gradients and hessians and third derivatives up to Lmax. More... and their gradients and hessians and third derivatives up to Lmax. More... | |
| int | index (int l, int m) const |
returns the index/locator for ( 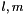 ) combo, ) combo, 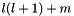 More... More... | |
| value_type | getYlm (int l, int m) const |
returns the value of  given given 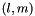 More... More... | |
| Point_t | getGradYlm (int l, int m) const |
returns the gradient of  given given 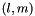 More... More... | |
| Tensor_t | getHessYlm (int l, int m) const |
returns the hessian of  given given 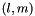 More... More... | |
| GGG_t | getGGGYlm (int lm) const |
returns the matrix of third derivatives of  given given 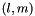 More... More... | |
| value_type | getYlm (int lm) const |
returns the value of  given given 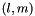 More... More... | |
| Point_t | getGradYlm (int lm) const |
returns the gradient of  given given 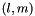 More... More... | |
| Tensor_t | getHessYlm (int lm) const |
returns the hessian of  given given 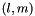 More... More... | |
| int | size () const |
| int | lmax () const |
Public Attributes | |
| int | Lmax |
| maximum angular momentum for the center More... | |
| std::vector< value_type > | Ylm |
values Ylm 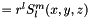 More... More... | |
| std::vector< value_type > | NormFactor |
| Normalization factors. More... | |
| std::vector< value_type > | FactorLM |
pre-evaluated factor 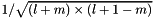 More... More... | |
| std::vector< value_type > | FactorL |
pre-evaluated factor 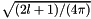 More... More... | |
| std::vector< value_type > | Factor2L |
pre-evaluated factor 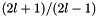 More... More... | |
| std::vector< Point_t > | gradYlm |
gradients gradYlm 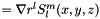 More... More... | |
| std::vector< hess_type > | hessYlm |
hessian hessYlm 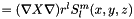 More... More... | |
| std::vector< value_type > | laplYlm |
| mmorales: HACK HACK HACK, to avoid having to rewrite QMCWaveFunctions/SphericalBasisSet.h More... | |
| std::vector< ggg_type > | gggYlm |
SphericalTensor that evaluates the Real Spherical Harmonics.
The template parameters
Real Spherical Harmonics Ylm 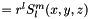 is stored in an array ordered as [0,-1 0 1,-2 -1 0 1 2, -Lmax,-Lmax+1,..., Lmax-1,Lmax] where Lmax is the maximum angular momentum of a center. All the data members, e.g, Ylm and pre-calculated factors, can be accessed by index(l,m) which returns the locator of the combination for l and m.
is stored in an array ordered as [0,-1 0 1,-2 -1 0 1 2, -Lmax,-Lmax+1,..., Lmax-1,Lmax] where Lmax is the maximum angular momentum of a center. All the data members, e.g, Ylm and pre-calculated factors, can be accessed by index(l,m) which returns the locator of the combination for l and m.
Definition at line 40 of file SphericalTensor.h.
| using ggg_type = GGG_t |
Definition at line 46 of file SphericalTensor.h.
| using hess_type = Tensor_t |
Definition at line 45 of file SphericalTensor.h.
| using pos_type = Point_t |
Definition at line 44 of file SphericalTensor.h.
| using This_t = SphericalTensor<T, Point_t> |
Definition at line 47 of file SphericalTensor.h.
| using value_type = T |
Definition at line 43 of file SphericalTensor.h.
|
explicit |
constructor
| l_max | maximum angular momentum |
| addsign | flag to determine what convention to use |
Evaluate all the constants and prefactors. The spherical harmonics is defined as
![\[ Y_l^m (\theta,\phi) = \sqrt{\frac{(2l+1)(l-m)!}{4\pi(l+m)!}} P_l^m(\cos\theta)e^{im\phi}\]](../../form_56.png)
Note that the data member Ylm is a misnomer and should not be confused with "spherical harmonics" 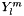 .
.
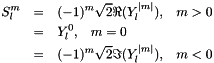
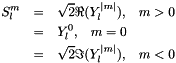
Definition at line 141 of file SphericalTensor.h.
References qmcplusplus::atan(), SphericalTensor< T, Point_t, Tensor_t, GGG_t >::Factor2L, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::FactorL, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::FactorLM, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::gggYlm, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::gradYlm, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::hessYlm, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::index(), SphericalTensor< T, Point_t, Tensor_t, GGG_t >::laplYlm, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::Lmax, qmcplusplus::Units::distance::m, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::NormFactor, pi, qmcplusplus::pow(), qmcplusplus::sqrt(), and SphericalTensor< T, Point_t, Tensor_t, GGG_t >::Ylm.
| void evaluate | ( | const Point_t & | p | ) |
makes a table of  and their gradients up to Lmax.
and their gradients up to Lmax.
Definition at line 233 of file SphericalTensor.h.
References qmcplusplus::atan(), qmcplusplus::Units::distance::m, pi, qmcplusplus::sqrt(), and Ylm().
| void evaluateAll | ( | const Point_t & | p | ) |
makes a table of  and their gradients up to Lmax.
and their gradients up to Lmax.
Definition at line 322 of file SphericalTensor.h.
References qmcplusplus::abs(), qmcplusplus::atan(), qmcplusplus::Units::distance::m, pi, qmcplusplus::sqrt(), and Ylm().
| void evaluateTest | ( | const Point_t & | p | ) |
makes a table of  and their gradients up to Lmax.
and their gradients up to Lmax.
Definition at line 713 of file SphericalTensor.h.
References SCTFunctor< SCT, L >::apply(), qmcplusplus::atan(), norm(), pi, qmcplusplus::sqrt(), and Ylm().
| void evaluateThirdDerivOnly | ( | const Point_t & | p | ) |
makes a table of  and their gradients and hessians and third derivatives up to Lmax.
and their gradients and hessians and third derivatives up to Lmax.
Definition at line 641 of file SphericalTensor.h.
| void evaluateWithHessian | ( | const Point_t & | p | ) |
makes a table of  and their gradients and hessians up to Lmax.
and their gradients and hessians up to Lmax.
Definition at line 481 of file SphericalTensor.h.
References qmcplusplus::abs(), qmcplusplus::atan(), qmcplusplus::Units::distance::m, pi, qmcplusplus::sqrt(), and Ylm().
|
inline |
returns the matrix of third derivatives of  given
given 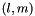
Definition at line 101 of file SphericalTensor.h.
References SphericalTensor< T, Point_t, Tensor_t, GGG_t >::gggYlm.
|
inline |
returns the gradient of  given
given 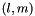
Definition at line 95 of file SphericalTensor.h.
References SphericalTensor< T, Point_t, Tensor_t, GGG_t >::gradYlm, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::index(), and qmcplusplus::Units::distance::m.
|
inline |
returns the gradient of  given
given 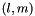
Definition at line 107 of file SphericalTensor.h.
References SphericalTensor< T, Point_t, Tensor_t, GGG_t >::gradYlm.
|
inline |
returns the hessian of  given
given 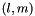
Definition at line 98 of file SphericalTensor.h.
References SphericalTensor< T, Point_t, Tensor_t, GGG_t >::hessYlm, SphericalTensor< T, Point_t, Tensor_t, GGG_t >::index(), and qmcplusplus::Units::distance::m.
|
inline |
returns the hessian of  given
given 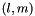
Definition at line 110 of file SphericalTensor.h.
References SphericalTensor< T, Point_t, Tensor_t, GGG_t >::hessYlm.
|
inline |
returns the value of  given
given 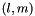
Definition at line 92 of file SphericalTensor.h.
References SphericalTensor< T, Point_t, Tensor_t, GGG_t >::index(), qmcplusplus::Units::distance::m, and SphericalTensor< T, Point_t, Tensor_t, GGG_t >::Ylm.
|
inline |
returns the value of  given
given 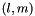
Definition at line 104 of file SphericalTensor.h.
References SphericalTensor< T, Point_t, Tensor_t, GGG_t >::Ylm.
|
inline |
returns the index/locator for ( 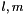 ) combo,
) combo, 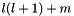
Definition at line 89 of file SphericalTensor.h.
References qmcplusplus::Units::distance::m.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::getGradYlm(), SphericalTensor< T, Point_t, Tensor_t, GGG_t >::getHessYlm(), SphericalTensor< T, Point_t, Tensor_t, GGG_t >::getYlm(), and SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
|
inline |
Definition at line 114 of file SphericalTensor.h.
References SphericalTensor< T, Point_t, Tensor_t, GGG_t >::Lmax.
|
inline |
Definition at line 112 of file SphericalTensor.h.
References SphericalTensor< T, Point_t, Tensor_t, GGG_t >::Ylm.
| std::vector<value_type> Factor2L |
pre-evaluated factor 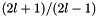
Definition at line 128 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
| std::vector<value_type> FactorL |
pre-evaluated factor 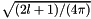
Definition at line 126 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
| std::vector<value_type> FactorLM |
pre-evaluated factor 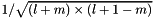
Definition at line 124 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
| std::vector<ggg_type> gggYlm |
Definition at line 137 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::getGGGYlm(), and SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
| std::vector<Point_t> gradYlm |
gradients gradYlm 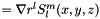
Definition at line 130 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::getGradYlm(), and SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
| std::vector<hess_type> hessYlm |
hessian hessYlm 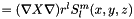
Definition at line 132 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::getHessYlm(), and SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
| std::vector<value_type> laplYlm |
mmorales: HACK HACK HACK, to avoid having to rewrite QMCWaveFunctions/SphericalBasisSet.h
Definition at line 135 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
| int Lmax |
maximum angular momentum for the center
Definition at line 117 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::lmax(), and SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
| std::vector<value_type> NormFactor |
Normalization factors.
Definition at line 122 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().
| std::vector<value_type> Ylm |
values Ylm 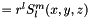
Definition at line 120 of file SphericalTensor.h.
Referenced by SphericalTensor< T, Point_t, Tensor_t, GGG_t >::getYlm(), SphericalTensor< T, Point_t, Tensor_t, GGG_t >::size(), and SphericalTensor< T, Point_t, Tensor_t, GGG_t >::SphericalTensor().