 |
QMCPACK
|
 |
QMCPACK
|
SoaSphericalTensor that evaluates the Real Spherical Harmonics. More...
 Inheritance diagram for SoaSphericalTensor< T >:
Inheritance diagram for SoaSphericalTensor< T >: Collaboration diagram for SoaSphericalTensor< T >:
Collaboration diagram for SoaSphericalTensor< T >:Public Member Functions | |
| SoaSphericalTensor (const int l_max, bool addsign=false) | |
| constructor More... | |
| SoaSphericalTensor (const SoaSphericalTensor &rhs)=default | |
| void | evaluateV (T x, T y, T z, T *Ylm) const |
| compute Ylm More... | |
| void | batched_evaluateV (const OffloadArray3D &xyz, OffloadArray3D &Ylm) const |
| evaluate V for multiple electrons and multiple pbc images More... | |
| void | batched_evaluateVGL (const OffloadArray3D &xyz, OffloadArray4D &Ylm_vgl) const |
| evaluate VGL for multiple electrons and multiple pbc images More... | |
| void | evaluateV (T x, T y, T z) |
| compute Ylm More... | |
| void | evaluateVGL (T x, T y, T z) |
makes a table of  and their gradients up to Lmax. More... and their gradients up to Lmax. More... | |
| void | evaluateVGH (T x, T y, T z) |
makes a table of  and their gradients up to Lmax. More... and their gradients up to Lmax. More... | |
| void | evaluateVGHGH (T x, T y, T z) |
makes a table of  and their gradients up to Lmax. More... and their gradients up to Lmax. More... | |
| const T * | operator[] (size_t component) const |
| return the starting address of the component More... | |
| size_t | size () const |
| int | lmax () const |
Static Public Member Functions | |
| static void | evaluate_bare (T x, T y, T z, T *Ylm, int lmax, const T *factorL, const T *factorLM) |
| compute Ylm for single position More... | |
| static void | evaluateVGL_impl (const T x, const T y, const T z, T *restrict Ylm_vgl, int lmax, const T *factorL, const T *factorLM, const T *factor2L, const T *normfactor, size_t offset) |
| compute Ylm_vgl for single position More... | |
| static int | index (int l, int m) |
returns the index/locator for ( 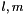 ) combo, ) combo, 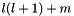 More... More... | |
Private Types | |
| using | OffloadVector = Vector< T, OffloadPinnedAllocator< T > > |
| using | OffloadArray2D = Array< T, 2, OffloadPinnedAllocator< T > > |
| using | OffloadArray3D = Array< T, 3, OffloadPinnedAllocator< T > > |
| using | OffloadArray4D = Array< T, 4, OffloadPinnedAllocator< T > > |
Private Attributes | |
| int | Lmax |
| maximum angular momentum for the center More... | |
| const std::shared_ptr< OffloadVector > | norm_factor_ptr_ |
| Normalization factors. More... | |
| const std::shared_ptr< OffloadVector > | factorLM_ptr_ |
pre-evaluated factor 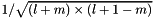 More... More... | |
| const std::shared_ptr< OffloadVector > | factorL_ptr_ |
pre-evaluated factor 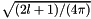 More... More... | |
| const std::shared_ptr< OffloadVector > | factor2L_ptr_ |
pre-evaluated factor 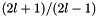 More... More... | |
| OffloadVector & | norm_factor_ |
| norm_factor reference More... | |
| OffloadVector & | factorLM_ |
| factorLM reference More... | |
| OffloadVector & | factorL_ |
| factorL reference More... | |
| OffloadVector & | factor2L_ |
| factor2L reference More... | |
| VectorSoaContainer< T, 5 > | cYlm |
| composite More... | |
SoaSphericalTensor that evaluates the Real Spherical Harmonics.
The template parameters
Real Spherical Harmonics Ylm 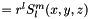 is stored in an array ordered as [0,-1 0 1,-2 -1 0 1 2, -Lmax,-Lmax+1,..., Lmax-1,Lmax] where Lmax is the maximum angular momentum of a center. All the data members, e.g, Ylm and pre-calculated factors, can be accessed by index(l,m) which returns the locator of the combination for l and m.
is stored in an array ordered as [0,-1 0 1,-2 -1 0 1 2, -Lmax,-Lmax+1,..., Lmax-1,Lmax] where Lmax is the maximum angular momentum of a center. All the data members, e.g, Ylm and pre-calculated factors, can be accessed by index(l,m) which returns the locator of the combination for l and m.
Definition at line 40 of file SoaSphericalTensor.h.
|
private |
Definition at line 44 of file SoaSphericalTensor.h.
|
private |
Definition at line 45 of file SoaSphericalTensor.h.
|
private |
Definition at line 46 of file SoaSphericalTensor.h.
|
private |
Definition at line 43 of file SoaSphericalTensor.h.
|
inlineexplicit |
constructor
| l_max | maximum angular momentum |
| addsign | flag to determine what convention to use |
Evaluate all the constants and prefactors. The spherical harmonics is defined as
![\[ Y_l^m (\theta,\phi) = \sqrt{\frac{(2l+1)(l-m)!}{4\pi(l+m)!}} P_l^m(\cos\theta)e^{im\phi}\]](../../form_56.png)
Note that the data member Ylm is a misnomer and should not be confused with "spherical harmonics" 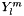 .
.
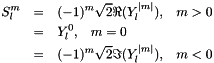
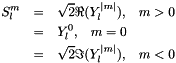
Definition at line 225 of file SoaSphericalTensor.h.
|
default |
|
inline |
evaluate V for multiple electrons and multiple pbc images
| [in] | xyz | electron positions [Nelec, Npbc, 3(x,y,z)] |
| [out] | Ylm | Spherical tensor elements [Nelec, Npbc, Nlm] |
Definition at line 101 of file SoaSphericalTensor.h.
|
inline |
evaluate VGL for multiple electrons and multiple pbc images
when offload is enabled, xyz is assumed to be up to date on the device before entering the function Ylm_vgl will be up to date on the device (but not host) when this function exits
| [in] | xyz | electron positions [Nelec, Npbc, 3(x,y,z)] |
| [out] | Ylm_vgl | Spherical tensor elements [5(v, gx, gy, gz, lapl), Nelec, Npbc, Nlm] |
Definition at line 140 of file SoaSphericalTensor.h.
|
inlinestatic |
compute Ylm for single position
Definition at line 288 of file SoaSphericalTensor.h.
Referenced by SoaSphericalTensor< ST >::batched_evaluateV(), and SoaSphericalTensor< ST >::evaluateV().
|
inline |
compute Ylm
Definition at line 88 of file SoaSphericalTensor.h.
Referenced by AtomicOrbitals< ST >::evaluate_v(), and AtomicOrbitals< ST >::evaluateValues().
|
inline |
compute Ylm
Definition at line 171 of file SoaSphericalTensor.h.
|
inline |
makes a table of  and their gradients up to Lmax.
and their gradients up to Lmax.
Definition at line 510 of file SoaSphericalTensor.h.
|
inline |
makes a table of  and their gradients up to Lmax.
and their gradients up to Lmax.
Definition at line 516 of file SoaSphericalTensor.h.
|
inline |
makes a table of  and their gradients up to Lmax.
and their gradients up to Lmax.
Definition at line 503 of file SoaSphericalTensor.h.
Referenced by AtomicOrbitals< ST >::evaluate_vgl().
|
inlinestatic |
compute Ylm_vgl for single position
Definition at line 392 of file SoaSphericalTensor.h.
Referenced by SoaSphericalTensor< ST >::batched_evaluateVGL().
|
inlinestatic |
|
inline |
Definition at line 199 of file SoaSphericalTensor.h.
|
inline |
return the starting address of the component
component=0(V), 1(dx), 2(dy), 3(dz), 4(Lap)
Definition at line 195 of file SoaSphericalTensor.h.
|
inline |
Definition at line 197 of file SoaSphericalTensor.h.
|
private |
composite
Definition at line 66 of file SoaSphericalTensor.h.
Referenced by SoaSphericalTensor< ST >::evaluateV(), SoaSphericalTensor< ST >::operator[](), and SoaSphericalTensor< ST >::size().
|
private |
factor2L reference
Definition at line 64 of file SoaSphericalTensor.h.
Referenced by SoaSphericalTensor< ST >::batched_evaluateVGL().
|
private |
pre-evaluated factor 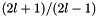
Definition at line 56 of file SoaSphericalTensor.h.
|
private |
factorL reference
Definition at line 62 of file SoaSphericalTensor.h.
Referenced by SoaSphericalTensor< ST >::batched_evaluateV(), SoaSphericalTensor< ST >::batched_evaluateVGL(), and SoaSphericalTensor< ST >::evaluateV().
|
private |
pre-evaluated factor 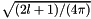
Definition at line 54 of file SoaSphericalTensor.h.
|
private |
factorLM reference
Definition at line 60 of file SoaSphericalTensor.h.
Referenced by SoaSphericalTensor< ST >::batched_evaluateV(), SoaSphericalTensor< ST >::batched_evaluateVGL(), and SoaSphericalTensor< ST >::evaluateV().
|
private |
pre-evaluated factor 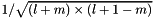
Definition at line 52 of file SoaSphericalTensor.h.
|
private |
maximum angular momentum for the center
Definition at line 48 of file SoaSphericalTensor.h.
Referenced by SoaSphericalTensor< ST >::batched_evaluateV(), SoaSphericalTensor< ST >::batched_evaluateVGL(), SoaSphericalTensor< ST >::evaluateV(), and SoaSphericalTensor< ST >::lmax().
|
private |
norm_factor reference
Definition at line 58 of file SoaSphericalTensor.h.
Referenced by SoaSphericalTensor< ST >::batched_evaluateV(), SoaSphericalTensor< ST >::batched_evaluateVGL(), and SoaSphericalTensor< ST >::evaluateV().
|
private |
Normalization factors.
Definition at line 50 of file SoaSphericalTensor.h.